新型コロナウイルスの感染拡大防止に向け、世界各国は感染状況に応じてさまざまな施策を行ってきている。三菱総合研究所では、代表的な感染症数理モデルであるSEIRモデル(Susceptible-Exposed-Infectious-Recovered)を用いて、各国における感染者数の状況および各種対応後の状況の定量的な把握と対策の効果分析を行った。
現時点で得られるデータは質的・量的に限定されており、その結果としてモデルに基づく分析結果は大きな不確実性を含むことに留意が必要である。不確実性の分析を含む分析手法の詳細については文末の別添をご参照いただきたい。
現時点で得られるデータは質的・量的に限定されており、その結果としてモデルに基づく分析結果は大きな不確実性を含むことに留意が必要である。不確実性の分析を含む分析手法の詳細については文末の別添をご参照いただきたい。
図1 SEIRモデル

出所:Iwata K, Miyakoshi C.(2020) A Simulation on Potential Secondary Spread of Novel Coronavirus in an Exported Country Using a Stochastic Epidemic SEIR Model. J Clin Med
本試算では、感染者に対する致死率が低く比較的対応が奏功しているドイツ、アイスランド、シンガポールを対象に、シミュレーションモデル(以下「モデル」)によって得られる値と公表データとが一致するように感染に関わる係数(以下「β」)を推計した。β は人から人への感染の速さを示す係数であり、対策の効果などにより時間的に変動することが予想されるため、今回の分析では、10日ごとに β を求めることとした。以下では、この β の値の変化から、各国の政策の効果を推し量り、考察を加えている。
図2 SEIRモデルで感染に関わる係数を変化させた結果(ドイツ)
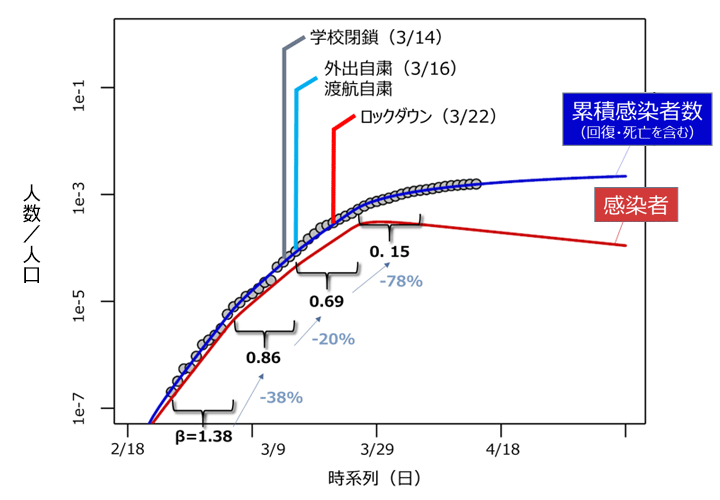
注:グラフの実線はモデル式を用いて推計した人口当たりの感染者数の推移。〇は公表データを示す。
出所:公表資料※1より三菱総合研究所作成
出所:公表資料※1より三菱総合研究所作成
図2はドイツを対象とした分析結果である。人口当たりの感染者数の増加率を規定するのが、感染に関わる係数 β である。ドイツについては、学校閉鎖、外出・渡航自粛、ロックダウンと対策を強化するにつれて、β で表される感染に関わる係数が確実に低下している。今回の分析結果からは、各対応が β に影響を与えるまで10日程度を要するように見える。ドイツでは4月20日以降、徐々に制限を緩和していくとしている。一人の感染者が何人を感染させるかを示す係数、いわゆる実効再生産数が現時点で1を切ったため、今後は感染者数そのものが減少していく可能性が出てきたと判断したのであろう。
図3 SEIRモデルで感染に関わる係数を変化させた結果(アイスランド)
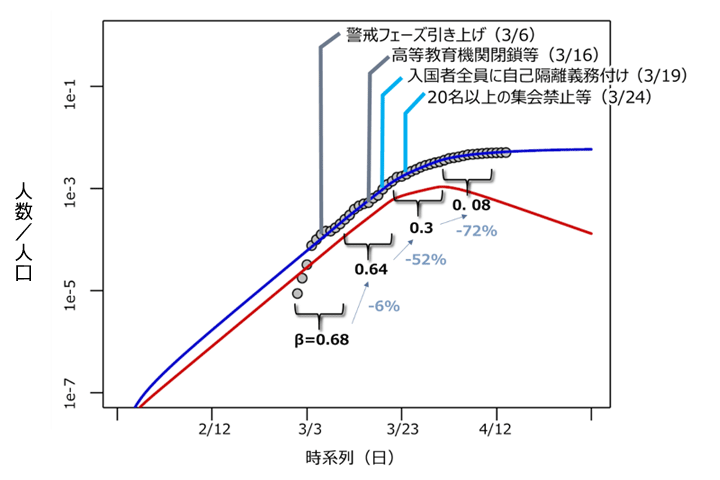
注:グラフの実線はモデル式を用いて推計した人口当たりの感染者数の推移。〇は公表データを示す。
出所:公表資料※1より三菱総合研究所作成
出所:公表資料※1より三菱総合研究所作成
アイスランドに対するシミュレーションにおいても、複数の対策が打たれた後に、感染に関わる係数 β が着実に低下している様子が見て取れる。アイスランド政府の発表によれば、アイスランド国内の感染者数の増加ペースは緩やかになっており、封じ込めおよび種々の流行対策の効果がみられるとしている。そのため、5月4日以降には対策を緩和していく予定となっている。
図4 シミュレーションによる今後の感染者数
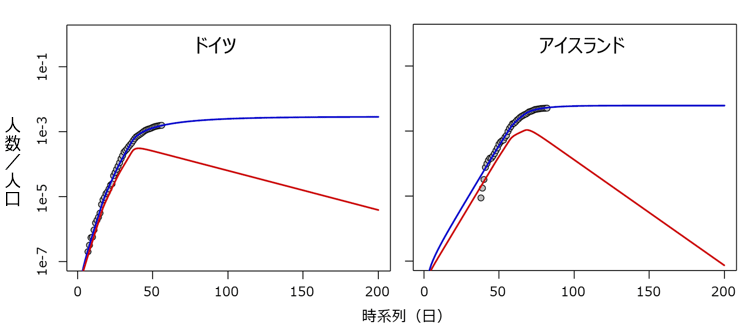
注:グラフの実線はモデル式を用いて推計した人口当たりの感染者数の推移。〇は公表データを示す。
出所:公表資料※1より三菱総合研究所作成
出所:公表資料※1より三菱総合研究所作成
参考までに、より長期における感染者数の変化も、直近の推計区間で求めた β を用いて試算した(図4)。なおこの試算では、季節的な変化やコロナウイルスの変異の可能性、今後の対策の緩和などは考慮していない。ドイツの場合、感染者数が減り始めてから4カ月程度でその数は1/10にまで減っている。アイスランドの場合、このまま推移すれば3カ月程度(ただし、シミュレーションでの誤差範囲は数カ月程度と大きい)で総人口に占める感染者の割合が非常に小さくなる試算結果となった。ただ、上述のとおり、両国における今後の対策の緩和などを見込んでいないため、実際の感染者数抑え込みにはより長期間を要する可能性は否定できない。
図5 SEIRモデルで感染に関わる係数を変化させた結果(シンガポール)
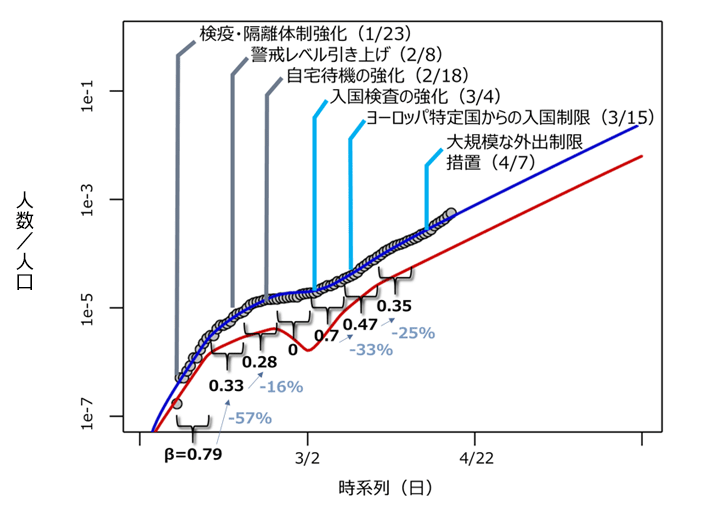
注:グラフの実線はモデル式を用いて推計した人口当たりの感染者数の推移。〇は公表データを示す。
出所:公表資料※1より三菱総合研究所作成
出所:公表資料※1より三菱総合研究所作成
感染者数増加の一時的な抑制に成功しても、再び増加が始まる例もある。たとえばシンガポールでは、コロナウイルスの流行が一時的には落ち着いたものの、その後、感染者数が再び増加する現象が見られている。今回のシミュレーションにおいても感染する係数 β がコロナウイルス流行の初期に戻っていることが分かる。この β が上昇し始めた頃から、入国制限などの厳しい対策が取られている。
各国とも感染状況に応じて接触制限措置を緩和している部分はあるが、段階を踏みながらの緩和であり、流行動態を注視しながら慎重に措置を取っていく方針のようだ。ドイツでは制限措置を緩和したものの、ミサなどの集会は8月末まで継続して開催を禁止するとしており、中長期的な警戒態勢をとる考えを示している。シンガポールのように、一旦流行が落ち着いたように見えても、再度感染者が増加するケースもある。
各国の状況を見ると、日本でも5月6日までの緊急事態宣言の後もすぐに元の生活に戻れるわけではなさそうだ。外出・渡航自粛といった接触制限措置は数カ月単位では収まらず、年単位になる可能性を想定しておくべきだろう。また感染者数が増加に転じた場合は再度の緊急事態宣言下での対応の可能性もある。ワクチンや特効薬が出ない限り、長い戦いが予想される。今後の経済活動は長期戦を前提に検討することが必要である。
各国の状況を見ると、日本でも5月6日までの緊急事態宣言の後もすぐに元の生活に戻れるわけではなさそうだ。外出・渡航自粛といった接触制限措置は数カ月単位では収まらず、年単位になる可能性を想定しておくべきだろう。また感染者数が増加に転じた場合は再度の緊急事態宣言下での対応の可能性もある。ワクチンや特効薬が出ない限り、長い戦いが予想される。今後の経済活動は長期戦を前提に検討することが必要である。